【算法】排序算法系列详解---归并排序

排序算法

想要理解排序算法，我们先得了解什么是分而治之思想，一种著名的递归式问题解决方案。很多算法中都用到了这种思想。

D&C 分而治之

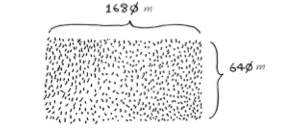
比方说我们有这样一块168 * 64的地皮，我们需要在尽可能大的情况下去均匀的分成正方形，求该正方形的边长。

所谓的分而治之就是把问题缩小化，大问题分成中等问题，中等问题分解成小问题来解决。

这道题我们可以通过不断的找正方形来慢慢分割出小问题来。先在这块地中划出64*64的正方形，那么剩余的地皮为40 * 64，再进行分割，如此往复…

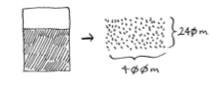
最终会得到一个8*8的方块，这个就是一个典型的分而治之思想。

归并排序

归并排序有两种，自顶向下和自底向上。

自顶向下算法思路

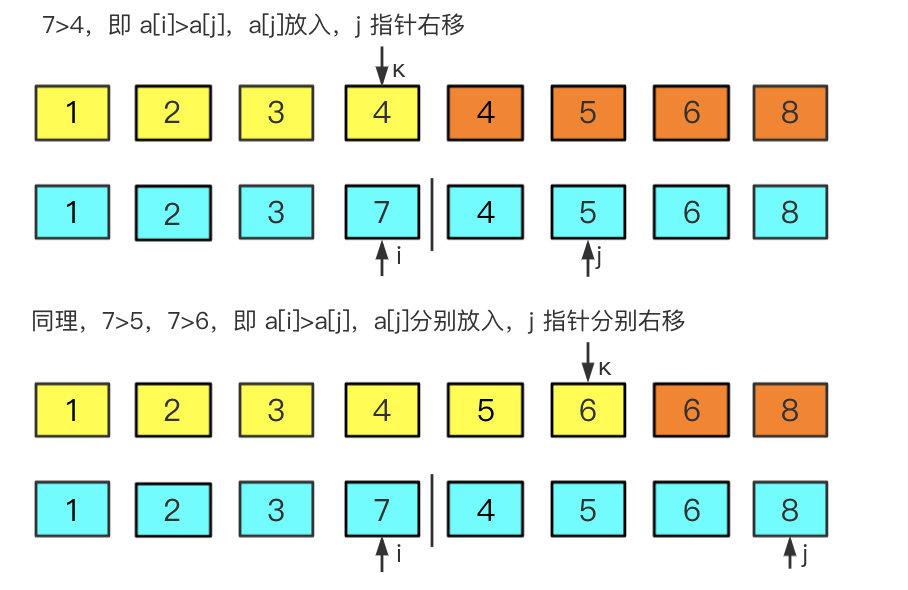
将数组拆分成两部分，先处理左边再处理右边，通过递归的方式对两边进行拆分，一直拆分到只有一个元素为止，然后再将两边的各元素进行比对，小的放前大的放后。过程如图：

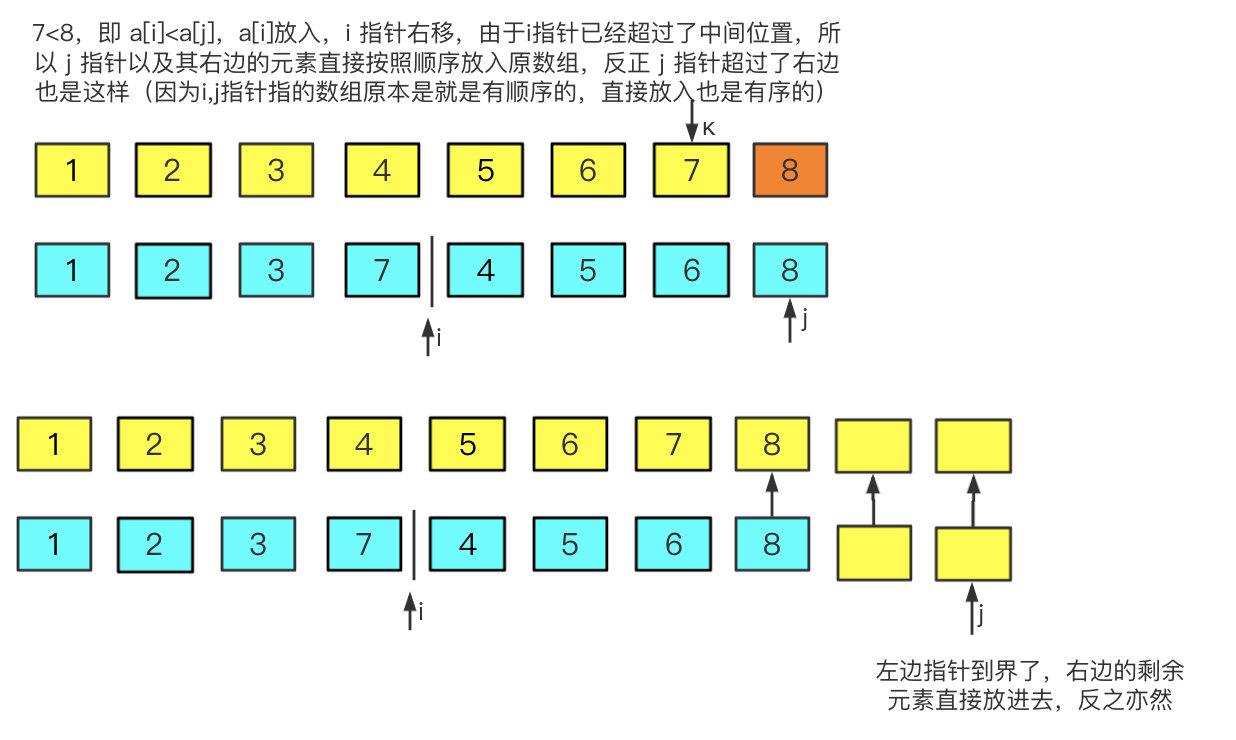
两组数组合并过程如图：

算法拆解

首先将无序的数组拆分成左右两部分
将两个数组分别逐一比对，左边的数组比对右边的数组
将较小的放入临时数组result中，并且从原数组中移除，循环结束条件为有一边的数组为空
按照这种思路对数组进行递归处理，从最小的数组开始排序慢慢延伸到整个数组

代码实现

def merge(left, right):
  result = []
  while len(left) > 0 and len(right) > 0:
    if left[0] <= right[0]: result.append(left.pop(0))
    else: result.append(right.pop(0))
  result += left
  result += right
  return result

def mergeSort(arr):
  if len(arr)==1: return arr
  mid = len(arr) // 2
  left = arr[:mid]
  right = arr[mid:]
  return merge(mergeSort(left), mergeSort(right))

时间复杂度分析

我们假设C(N)表示一个长度为N的数组在归并排序时需要比较的次数。我们知道C(0)=C(1)=0，对于N>0，通过递归的sort()方法我们可以由相应的归纳关系得到比较次数的上限：

C(N) ≤ C(N/2) + C(N/2) + N

右边的第一项是将数组的左半部分排序所用的比较次数，第二项是将数组的右半部分排序所用的比较次数，第三项是归并所用的比较次数。因为归并所需的比较次数最少为N/2，比较次数的下限是：

C(N) ≥ C(N/2) + C(N/2) + N/2

当N为2的幂（即N=2的n次方）且等号成立时我们能够得到一个解。首先，因为N/2下限 = N/2上限 = 2^n-1，可以得到：

C(2^n) = 2C(2^n-1)+2^n

将两边同时除以2^n可得：

C(2^n)/2^n = C(2^n-1)/2^n-2 +1+1

将上一步重复n-1遍可得:

C(2^n)/2^n = C(2^0)/2^0 + n

将两边同时乘以2^n就可以解得：

C(N) = C(2^n) = n2^n = NlogN

对于一般的N，得到的准确值要更复杂一些。但对比较次数的上下界不等式使用相同的方法不难证明前面所述的对于任意N的结论。

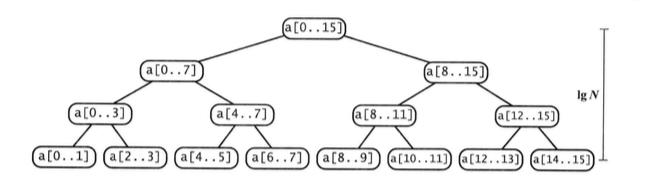
下图是N=16时，对于归并排序中子数组的依赖树

归并排序与快速排序的区别

相同点：

都采用分治算法
都可以递归实现
平均时间复杂度都是O(nlogn)

不同点：

归并排序是先切分、后排序，快速排序是切分、排序交替进行；
归并排序是稳定的排序，而快速排序是不稳定的排序；
归并排序在最坏和最好情况下的时间复杂度均为O(nlogn)，而快速排序最坏O(n^2)，最好O(n)；
快速排序是原地排序，归并不是。

loannes's blog