146. LRU 缓存机制

前言

今天在刷leetcode的时候，遇到了LRU缓存机制的问题。觉得很有意思，就准备把这道题的题解以及相关知识点记录下来。

原题是这样的

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作：获取数据 get 和写入数据 put 。

获取数据 get(key) - 如果关键字 (key) 存在于缓存中，则获取关键字的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字/值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

结合实际场景来分析这道题的话就是我们现在有一个空间有限的缓存池，为了保证缓存不会溢出我们需要定时将缓存中长时间未使用或者最近次数用的最少的单位给清理掉。其实看到这里的时候我第一个联想到的就是iOS的任务管理器（虽然它现在做的是假后台，app在一段时间后会自动从缓存中清除），但是在以前它就是这么做的。

常见的缓存淘汰策略

其实常见的缓存淘汰策略不止LRU，但是其他两种都非常简单。利用队列或者哈希表就能实现了，所以这里只分析LRU。

先进先出策略 FIFO（First In，First Out）队列
最少使用策略 LFU（Least Frequently Used）哈希表
最近最少使用策略 LRU（Least Recently Used）哈希表 + 双向链表

什么是LRU缓存机制

下面以图解的方式来解释下什么是LRU。

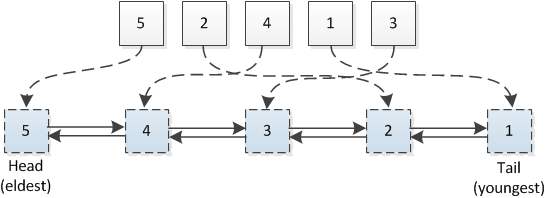
LRU的缓存机制简单来讲就是哈希表 + 双向链表，也就是Python3中的OrderedDict。我们通过哈希表来保证最基本的set与get功能外，需要借助双向链表来保证缓存中存储着固定数量的数据，在需要删除数据的时候能在O(1)的时间复杂度下找到这条数据。而get访问能及时的更新这条数据的使用情况，对数据的使用量做出排序。

实现部分

先实现一个双向链表的节点类，为什么要使用双向链表而不是单向链表？如果用单向链表，没办法快速定位到尾部节点，这样在做删除操作的时候时间复杂度将会变为O(N)。

class DLinkedNode:
    def __init__(self, key=0, value=0):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None

缓存初始化

为了将时间复杂度优化到O(1)，需要使用链表的head(头部)和tail(尾部)两部分，需要指定容器的界限capacity。

class LRUCache:
    def __init__(self, capacity: int):
        self.cache = dict()
        self.head = DLinkedNode()
        self.tail = DLinkedNode()
        self.head.next = self.tail
        self.tail.prev = self.head
        self.capacity = capacity
        self.size = 0

get/put部分

在python中为了避免关键字冲突，将set函数改为了put。

该部分逻辑：

获取操作时，表示访问了该数据，数据被使用了一次，移动到了链表最前面。
插入操作时，判断是否超出了容器上限，如果超过就需要删除链表末尾的数据(表示最近使用最少的将被淘汰)，并将新数据放入到链表最前面。

def get(self, key: int) -> int:
        if key not in self.cache:
            return -1
        node = self.cache[key]
        self.moveToHead(node)
        return node.value

    def put(self, key: int, value: int) -> None:
        if key not in self.cache:
            node = DLinkedNode(key, value)
            self.cache[key] = node
            self.addToHead(node)
            self.size += 1
            if self.size > self.capacity:
                removed = self.removeTail()
                self.cache.pop(removed.key)
                self.size -= 1
        else:
            node = self.cache[key]
            node.value = value
            self.moveToHead(node)

剩余部分

这里没什么好说明的，都是最简单是链表操作部分。

添加到链表头部
删除指定节点
移动到头部
删除尾部数据

    def addToHead(self, node):
        node.prev = self.head
        node.next = self.head.next
        self.head.next.prev = node
        self.head.next = node
    
    def removeNode(self, node):
        node.prev.next = node.next
        node.next.prev = node.prev
    
    def moveToHead(self, node):
        self.removeNode(node)
        self.addToHead(node)
    
    def removeTail(self):
        node = self.tail.prev
        self.removeNode(node)
        return node

loannes's blog